1. Poker Probability Straight Flush Valve
2. Poker Probability Straight Flush Rules
3. Probability Of Straight Flush Poker
4. Poker Probability Straight Flush Lines

Discover the numbers, strategy and odds behind the Straight Flush and the poker odds of flopping the top-best hand in poker. Thus, only seven more cards will help you to complete your flush. Your chance to shape the winning hand on the turn is therefore 15/47 = 31.9%. For advanced poker players: what is the probability of making the winning hand from the flop to the river (straight or a flush) in the above situation?

The tables below show the probabilities of being dealt various poker hands with different wild card specifications. Each Poker hand consists of selecting the 5 best cards from a random 7 card deal.
While probabilities for the best 5 card hand from a deal of 7 cards (but no wild cards) can be calculated via direct combinatorics, the introduction of wild cards greatly complicates the combinatoric calculations. Thus, to produce the results shown here, the author wrote a computer program that would generate all possible poker hands. Each of these poker hands was evaluated for matched ranks (pairs, 3 of a kind, etc.), straights, and flushes. Wild cards introduce multiple evaluations for a given hand, and the best standard evaluation for any given hand is used in the tables.
Data from this page may be freely used provided it includes an acknowledgement to the author.
7 card poker probabilities if there are no wild cards
(Computer program and data by Bill Butler)
Poker Hand Nbr. of Hands Probability
----------------------------------------------------
5 of a kind 0 0.00000000
Royal straight flush 4,324 0.00003232
Other straight flush 37,260 0.00027851
4 of a kind 224,848 0.00168067
Full House 3,473,184 0.02596102
Flush 4,047,644 0.03025494
Ace high straight 747,980 0.00559093
Other straights 5,432,040 0.04060289
3 of a kind 6,461,620 0.04829870
2 pairs 31,433,400 0.23495536
One pair >= Jacks 18,188,280 0.13595201
One pair <= Tens 40,439,520 0.30227345
Ace high 12,944,820 0.09675870
King high 6,386,940 0.04774049
Queen high 2,719,500 0.02032746
Jack high 963,480 0.00720173
Ten high 248,640 0.00185851
Nine high 31,080 0.00023231
Subtotals high card only 23,294,460 0.17411920
Total = 133,784,560 1.00000000
= COMBIN(52,7)
(Interesting observation: If a hand evaluates to just one pair, it is not distributed 4/13 “Jacks or better”. If you have a single middle-sized pair, you have a slightly increased chance of also having a straight which evaluates to a better hand. Thus a middle-sized pair occurs slightly less often than a high (Jacks or better) or a low (5’s or lower) pair.)
7 card poker probabilities if one “Pai Gow” (“Bug”) Joker is added to the deck
A “Pai Gow” (“Bug”) Joker is partially wild. If you are using it to complete a straight and/or a flush, it is an ordinary wild card. If you are using it for pairs, 3-of-a-kind, etc., it is forced to be an Ace.
(Computer program and data by Bill Butler)
Poker Hand Nbr. of Hands Probability
----------------------------------------------------
5 Aces 1,128 0.00000732
Royal straight flush 26,132 0.00016953
Other straight flush 184,832 0.00119909
4 of a kind 307,472 0.00199472
Full House 4,188,528 0.02717299
Flush 6,172,088 0.04004129
Ace high straight 1,554,156 0.01008255
Other straights 9,681,872 0.06281094
3 of a kind 7,470,676 0.04846585
2 pairs 35,553,816 0.23065464
One pair >= Jacks 19,273,104 0.12503386
One pair <= Tens 44,948,856 0.29160476
Ace high 14,430,780 0.09361938
King high 6,386,940 0.04143514
Queen high 2,719,500 0.01764270
Jack high 963,480 0.00625056
Ten high 248,640 0.00161305
Nine high 31,080 0.00020163
Subtotals high card only 24,780,420 0.16076246
Total = 154,143,080 1.00000000
= COMBIN(53,7)
7 card poker probabilities if one ordinary Joker is added to the deck
(Computer program and data by Bill Butler)
Poker Hand Nbr. of Hands Probability
----------------------------------------------------
5 of a kind 14,664 0.00009513
Royal straight flush 26,132 0.00016953
Other straight flush 184,832 0.00119909
4 of a kind 1,121,024 0.00727262
Full House 5,997,144 0.03890635
Flush 6,027,224 0.03910149
Ace high straight 1,543,460 0.01001316
Other straights 9,540,480 0.06189366
3 of a kind 13,315,300 0.08638273
2 pairs 31,433,400 0.20392352
One pair >= Jacks 21,170,640 0.13734408
One pair <= Tens 40,474,320 0.26257630
Ace high 12,944,820 0.08397925
King high 6,386,940 0.04143514
Queen high 2,719,500 0.01764270
Jack high 963,480 0.00625056
Ten high 248,640 0.00161305
Nine high 31,080 0.00020163
Subtotals high card only 23,294,460 0.15112232
Total = 154,143,080 1.00000000
= COMBIN(53,7)
7 card poker probabilities if two Jokers are added to the deck
(Computer program and data by Bill Butler)
Poker Hand Nbr. of Hands Probability
----------------------------------------------------
5 of a kind 88,608 0.00050033
Royal straight flush 91,764 0.00051815
Other straight flush 548,196 0.00309539
4 of a kind 3,134,544 0.01769923
Full House 8,521,104 0.04811449
Flush 8,397,324 0.04741557
Ace high straight 2,531,540 0.01429436
Other straights 14,181,120 0.08007383
3 of a kind 20,216,380 0.11415198
2 pairs 31,433,400 0.17748899
One pair >= Jacks 24,153,000 0.13638014
One pair <= Tens 40,509,120 0.22873513
Ace high 12,944,820 0.07309305
King high 6,386,940 0.03606392
Queen high 2,719,500 0.01535568
Jack high 963,480 0.00544030
Ten high 248,640 0.00140395
Nine high 31,080 0.00017549
Subtotals high card only 23,294,460 0.13153239
Total = 177,100,560 1.00000000
= COMBIN(54,7)
7 card poker probabilities with One-eyed Jacks wild
(Computer program and data by Bill Butler)

Poker Probability Straight Flush Valve

Poker Hand Nbr. of Hands Probability
----------------------------------------------------
5 of a kind 75,072 0.00056114
Royal straight flush 54,508 0.00040743
Other straight flush 447,946 0.00334826
4 of a kind 2,552,718 0.01908081
Full House 6,733,344 0.05032975
Flush 6,388,172 0.04774970
Ace high straight 1,404,464 0.01049795
Other straights 11,201,130 0.08372513
3 of a kind 15,758,140 0.11778743
2 pairs 23,810,436 0.17797596
One pair >= Jacks 16,255,890 0.12150797
One pair <= Tens 32,047,590 0.23954625
Ace high 9,743,580 0.07283038
King high 4,662,000 0.03484707
Queen high 1,888,110 0.01411306
Jack high 481,740 0.00360086
Ten high 248,640 0.00185851
Nine high 31,080 0.00023231
Subtotals high card only 17,055,150 0.12748220
Total = 133,784,560 1.00000000
= COMBIN(52,7)
7 card poker probabilities with Deuces (2’s) wild
(Computer program and data by Bill Butler)
Poker Hand Nbr. of Hands Probability
----------------------------------------------------
5 of a kind 609,760 0.00455778
Royal straight flush 399,484 0.00298602
Other straight flush 1,552,732 0.01160621
4 of a kind 7,504,920 0.05609706
Full House 9,421,824 0.07042535
Flush 7,993,600 0.05974979
Ace high straight 4,033,160 0.03014668
Other straights 15,355,640 0.11477887
3 of a kind 20,151,920 0.15062964
2 pairs 19,491,840 0.14569574
One pair >= Jacks 16,211,160 0.12117362
One pair <= Tens 20,708,880 0.15479275
Ace high 6,386,940 0.04774049
King high 2,719,500 0.02032746
Queen high 963,480 0.00720173
Jack high 248,640 0.00185851
Ten high 31,080 0.00023231
Nine high 0 0.00000000
Subtotals high card only 10,349,640 0.07736050
Total = 133,784,560 1.00000000
= COMBIN(52,7)
7 card poker probabilities with 2 Jokers,
One-eyed Jacks, and Deuces (2’s) wild
(8 out of 54 cards are wild)
(Computer program and data by Bill Butler)
Poker Hand Nbr. of Hands Probability
----------------------------------------------------
5 of a kind 5,496,072 0.03103362
Royal straight flush 1,821,704 0.01028627
Other straight flush 6,959,976 0.03929957
4 of a kind 23,628,576 0.13341898
Full House 12,751,424 0.07200104
Flush 13,497,668 0.07621471
Ace high straight 6,037,238 0.03408932
Other straights 25,527,008 0.14413849
3 of a kind 28,206,968 0.15927091
2 pairs 14,381,496 0.08120525
One pair >= Jacks 15,378,900 0.08683711
One pair <= Tens 16,024,260 0.09048114
Ace high 4,693,080 0.02649952
King high 1,911,420 0.01079285
Queen high 629,370 0.00355374
Jack high 124,320 0.00070197
Ten high 31,080 0.00017549
Nine high 0 0.00000000
Subtotals high card only 7,389,270 0.04172358
Total = 177,100,560 1.00000000
= COMBIN(54,7)

Poker Probability Straight Flush Rules

Alsoplease see 5 card Poker probabilities
Alsoplease see 6 card Poker probabilities
Alsoplease see 8 card, 9 card, and 10 card Poker probabilities
Return to the main Poker probabilities page
Return to Durango Bill’s home page
Web page generated via Sea Monkey's Composer HTML editor
within a Linux Cinnamon Mint 18 operating system.
(Goodbye Microsoft)

POKER PROBABILITIES

• Texas Hold'em Poker
  Texas Hold'em Poker probabilities
• Omaha Poker
  Omaha Poker probabilities
• 5 Card Poker
  5 Card Poker probabilities

POKER CALCULATOR

• Poker calculator
  Poker odds calculator

POKER INFORMATION

• Poker hand rankings
  Ranking of poker hands

Probability Of Straight Flush Poker

In poker, the probability of each type of 5-card hand can be computed by calculating the proportion of hands of that type among all possible hands.

Frequency of 5-card poker hands

The following enumerates the (absolute) frequency of each hand, given all combinations of 5 cards randomly drawn from a full deck of 52 without replacement. Wild cards are not considered. The probability of drawing a given hand is calculated by dividing the number of ways of drawing the hand by the total number of 5-card hands (the sample space, five-card hands). The odds are defined as the ratio (1/p) - 1 : 1, where p is the probability. Note that the cumulative column contains the probability of being dealt that hand or any of the hands ranked higher than it. (The frequencies given are exact; the probabilities and odds are approximate.)

The nCr function on most scientific calculators can be used to calculate hand frequencies; entering ​nCr​ with ​52​ and ​5​, for example, yields as above.

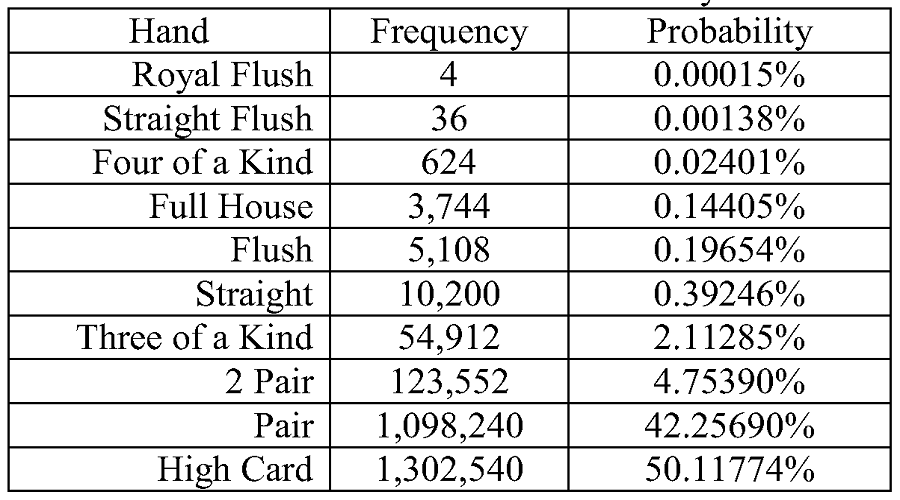
Hand	Frequency	Approx. Probability	Approx. Cumulative	Approx. Odds	Mathematical expression of absolute frequency
Royal flush	4	0.000154%	0.000154%	649,739 : 1
Straight flush (excluding royal flush)	36	0.00139%	0.00154%	72,192.33 : 1
Four of a kind	624	0.0240%	0.0256%	4,164 : 1
Full house	3,744	0.144%	0.170%	693.2 : 1
Flush (excluding royal flush and straight flush)	5,108	0.197%	0.367%	507.8 : 1
Straight (excluding royal flush and straight flush)	10,200	0.392%	0.76%	253.8 : 1
Three of a kind	54,912	2.11%	2.87%	46.3 : 1
Two pair	123,552	4.75%	7.62%	20.03 : 1
One pair	1,098,240	42.3%	49.9%	1.36 : 1
No pair / High card	1,302,540	50.1%	100%	.995 : 1
Total	2,598,960	100%	100%	1 : 1

The royal flush is a case of the straight flush. It can be formed 4 ways (one for each suit), giving it a probability of 0.000154% and odds of 649,739 : 1.

When ace-low straights and ace-low straight flushes are not counted, the probabilities of each are reduced: straights and straight flushes each become 9/10 as common as they otherwise would be. The 4 missed straight flushes become flushes and the 1,020 missed straights become no pair.

Note that since suits have no relative value in poker, two hands can be considered identical if one hand can be transformed into the other by swapping suits. For example, the hand 3♣ 7♣ 8♣ Q♠ A♠ is identical to 3♦ 7♦ 8♦ Q♥ A♥ because replacing all of the clubs in the first hand with diamonds and all of the spades with hearts produces the second hand. So eliminating identical hands that ignore relative suit values, there are only 134,459 distinct hands.

The number of distinct poker hands is even smaller. For example, 3♣ 7♣ 8♣ Q♠ A♠ and 3♦ 7♣ 8♦ Q♥ A♥ are not identical hands when just ignoring suit assignments because one hand has three suits, while the other hand has only two—that difference could affect the relative value of each hand when there are more cards to come. However, even though the hands are not identical from that perspective, they still form equivalent poker hands because each hand is an A-Q-8-7-3 high card hand. There are 7,462 distinct poker hands.

Derivation of frequencies of 5-card poker hands

of the binomial coefficients and their interpretation as the number of ways of choosing elements from a given set. See also: sample space and event (probability theory).

• Straight flush — Each straight flush is uniquely determined by its highest ranking card; and these ranks go from 5 (A-2-3-4-5) up to A (10-J-Q-K-A) in each of the 4 suits. Thus, the total number of straight flushes is:
  • Royal straight flush — A royal straight flush is a subset of all straight flushes in which the ace is the highest card (ie 10-J-Q-K-A in any of the four suits). Thus, the total number of royal straight flushes is

    or simply . Note: this means that the total number of non-Royal straight flushes is 36.

• Four of a kind — Any one of the thirteen ranks can form the four of a kind by selecting all four of the suits in that rank. The final card can have any one of the twelve remaining ranks, and any suit. Thus, the total number of four-of-a-kinds is:

• Full house — The full house comprises a triple (three of a kind) and a pair. The triple can be any one of the thirteen ranks, and consists of three of the four suits. The pair can be any one of the remaining twelve ranks, and consists of two of the four suits. Thus, the total number of full houses is:

• Flush — The flush contains any five of the thirteen ranks, all of which belong to one of the four suits, minus the 40 straight flushes. Thus, the total number of flushes is:

• Straight — The straight consists of any one of the ten possible sequences of five consecutive cards, from 5-4-3-2-A to A-K-Q-J-10. Each of these five cards can have any one of the four suits. Finally, as with the flush, the 40 straight flushes must be excluded, giving:

• Three of a kind — Any of the thirteen ranks can form the three of a kind, which can contain any three of the four suits. The remaining two cards can have any two of the remaining twelve ranks, and each can have any of the four suits. Thus, the total number of three-of-a-kinds is:

• Two pair — The pairs can have any two of the thirteen ranks, and each pair can have two of the four suits. The final card can have any one of the eleven remaining ranks, and any suit. Thus, the total number of two-pairs is:

• Pair — The pair can have any one of the thirteen ranks, and any two of the four suits. The remaining three cards can have any three of the remaining twelve ranks, and each can have any of the four suits. Thus, the total number of pair hands is:

• No pair — A no-pair hand contains five of the thirteen ranks, discounting the ten possible straights, and each card can have any of the four suits, discounting the four possible flushes. Alternatively, a no-pair hand is any hand that does not fall into one of the above categories; that is, any way to choose five out of 52 cards, discounting all of the above hands. Thus, the total number of no-pair hands is:

• Any five card poker hand — The total number of five card hands that can be drawn from a deck of cards is found using a combination selecting five cards, in any order where n refers to the number of items that can be selected and r to the sample size; the '!' is the factorial operator:

This guide is licensed under the GNU Free Documentation License. It uses material from the Wikipedia.

Poker Probability Straight Flush Lines

Home > 5 Card Poker probabilities